|
Schatten rotierender Schwarzer Löcher
|
|
Obwohl ein Schwarzes Loch nicht sichtbar ist, kann man es dennoch beobachten - es wirft einen Schatten, wenn es sich vor einem hellen Hintergrund befindet. Bereits seit den frühen 1970'er Jahren (Bardeen 1973, Luminet 1979, Quien et al. 1995, Hollywood und Melia 1997, Falcke et al. 2000, Bromley et al. 2001) wurden die scheinbaren Formen spezieller Schwarzer Löcher berechnet, de Vries (2000) erstellte Plots von Schatten allgemeiner rotierender und elektrisch geladener Schwarzer Löcher, in Abhängigkeit von ihrem Drehimpuls und ihrer Ladung. Sie können den folgenden Button drücken, um solche Plots berechnen zu lassen.
Im Weiteren wird kurz erklärt: Wie kann man solche Schattenumrisse bestimmen? Was sind die grundlegenden Prinzipien dieser Berechnungen?
Geometrische Optik
Im Kern basiert die Berechnung der scheinbaren Gestalt eines allgemeinen Schwarzen Lochs auf der geometrischen Optik: eine elektromagnetische Welle bewegt sich näherungsweise auf einer Schar von Lichtstrahlen fort, die senkrecht zu den Wellenfronten stehen. Gemäß der Allgemeinen Relativität nun sind Lichtstrahlen gebogene Kurven in einer durch vorhandene Massen gekrümmten Raumzeit.
Damit jedoch die Näherung der geometrischen Optik gültig ist, muss die Wellenlänge λ klein sein im Verhältnis zu dem typischen Krümmungsradius des Raumzeitgebiets. Für ein Schwarzes Loch von Sonnenmasse beispielsweise beträgt der Radius r+ des so genannten Ereignishorizonts (der "Rand" des Schwarzen Lochs) etwa 1,5 km, d.h., er ist von der Größenordnung des Krümmungsradius in der Umgebung des Horizonts. Somit ist für Mittelwellenstrahlung (mit λ zwischen 100 m und 1 km), die in Horizontnähe entsteht, die geometrische Optik keine gute Näherung, aber für etwas höherfrequente Radiotrahlung sehr wohl, erst recht für kürzere Wellen wie Infrarot, Licht oder gar Röntgenstrahlung.
Für das Zentrum unserer Milchstraße, mutmaßlich ein riesiges Schwarzes Loch von etwa 2,6 Mio Sonnenmassen, beträgt der Krümmungsradius etwa 4 Mio km, d.h. der Messfehler einer langwelligen Quelle (λ um 10 km) ist etwa 1:400000.
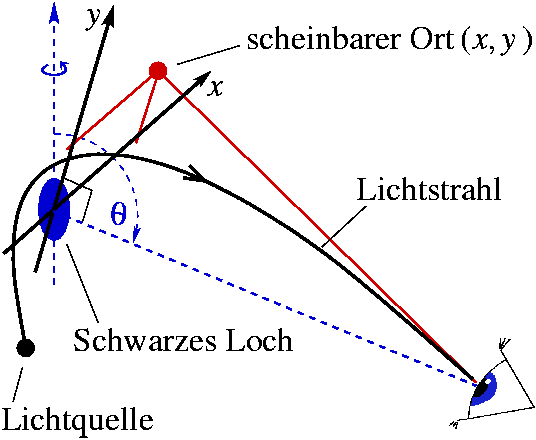
Nehmen wir die Ungenauigkeit der geometrischen Optik in Kauf, so erfahren wir die Welt um uns herum als eine optische Täuschung. Da die Lichtstrahlen, die einen Beobachter im unendlich Fernen erreichen, gekrümmt sind, scheinen sie aus einer ganz anderen Richtung zu kommen. Um den scheinbaren Ort einer Lichtquelle in der projizierten Himmelsfläche des Beobachters darzustellen, werden die Koordinaten (x, y) wie aus der folgenden Abbildung ersichtlich verwendet:
 |
|
Fig. 1.
Die (x,y)-Koordinaten, die den scheinbaren Ort eines
Lichstrahls bezüglich der projizierten, das Zentrum der
Raumzeit beinhaltenden Ebene lotrecht zum Beobachter
angeben: x bezeichnet den scheinbaren Abstand von der
Rotationsachse, und y die Projektion der
Rotationsachse (gestrichelte Linie) selbst.
|
Geschlossene Photonenbahnen
Eine genauere Analyse der Lichstrahlen in einer allgemeinen Kerr-Newman-Raumzeit (einer Verallgemeinerung rotierender und elektrisch geladener Schwarzer Löcher) mit einer Singularität zeigt, dass es Photonen gibt, die sich auf geschlossenen Bahnen bewegen (Bardeen 1973, Chandrasekhar 1983, de Vries 2000), also auf Ellipsen. Solche Bahnen beschreiben den Grenzwert der innersten Photonenbahnen, die aus dem Unendlichen kommend wieder zurück ins Unendliche entkommen. (Hier bedeutet das "Unendliche" das asymptotisch flache Gebiet weit entfernt von dem Schwarzen Loch; allerdings beträgt in einer Distanz von etwa dem 25-fachen des Ereignishorizonts r+ der Krümmungsradius R = 125r+, d.h. asymptotisch flache Raumzeitregionen werden recht schnell erreicht.)
Für einen Beobachter im unendlich Fernen, der ein Schwarzes Loch vor einem leuchtenden Hintergrund sieht, wirft es somit einen Schatten, der in der Näherung der geometrischen Optik durch die Menge der geschlossenen Photonenbahnen gegeben ist.
de Vries (2000) analysierte das
nichtlineare Differentialgleichungssystem, das geschlossen
Photonenbahnen bestimmt. Er fand heraus, dass für eine
Kerr-Newman-Raumzeit (einer Verallgemeinerung eines Schwarzen
Lochs)mit Masse M,
Drehimpuls a und elektrischer Ladung Q,
der scheinbare Ort eines auf einer geschlossenen Bahn
vom Radius r in den Koordinaten
(x, y) eines asymptotischen Beobachters
in dem Breitenkreis
![]() durch die folgenden recht komplizierten Formeln gegeben ist:
durch die folgenden recht komplizierten Formeln gegeben ist:
| x = | rD + rQ2 - M (r2 - a2) |
|
a (r-M) sin |
| y2 = | 4r2D |
- ( x - a sin |
| (r-M)2 |
mit D = r2 - 2Mr + a2 + Q2. Für Parameter, die die "kosmische Zensur" (Penrose 1979) erfüllen, die so genannte nackte Singularitäten verhindert, nämlich M2 ≤ a2 + Q2 (de Vries and Schmidt-Kaler 2002), ergeben diese Formeln wohldefinierte geschlossene Kurven auf der Himmelskugel des Beobachters, die Schattenkurven Schwarzer Löcher. Bitte drücken Sie den folgenden Button, um solche Schattenkurven berechnen zu lassen.
Falls Sie direkt über dieser Zeile nur eine graue Fläche sehen, jedoch keinen anklickbaren Button, so ist die Ursache, dass Sie nicht das neueste Java-Plug-In in Ihrem Browser installiert haben. Das Applet basiert auf den Java-2 Klassen (Swing), d.h. um es zu verwenden benötigen Sie die Java-Version 1.3 oder höher. Sie können das Plug-In bei SUN frei downloaden:
http://java.sun.com/getjava/download.html
oder
http://java.sun.com/products/plugin/
Literatur
- Bardeen, J., 1973. 'Timelike and null geodesics in the Kerr metric', in: De Witt, C., and De Witt, B.S., (eds.), Black Holes. École d'été de Physique Théorique, Les Houches 1972, 215-239. Gordon & Breach Science Publishers, New York
- Bromley, B.C., Melia, F., and Liu, S., 2001. 'Polarimetric Imaging of the Massive Black Hole at the Galactic Center', Astrophysical J., 555 L83-L86
- Chandrasekhar, S., 1998. The Mathematical Theory of Black Holes. Oxford University Press, Oxford
- Falcke, H., Melia, F., and Agol, E., 2000. 'Viewing the shadow of the black hole at the galactic center', Astrophys. J., 528, L13-L16. Siehe auch www.mpg.de/pri00/sld1.html
- Hollywood, J.M., and Melia, F., 1997. 'General relativistic effects on the infrared spectrum of thin accretion disks in active galactic nuclei: application to Sagittarius A*', Astrophys. J. Suppl. Ser., 112 423-455
- Luminet, J.P., 1979. 'Image of of a spherical black hole with thin accretion disk', Astron. Astrophys., 75, 228-235
- Penrose, R., 1979. 'Singularities and time asymmetry', in: Hawking, S.W., and Israel, W., (eds.), General Relativity. An Einstein Centenary Survey, Cambridge University Press, Cambridge
- Quien, N., Wehrse, R., and Kindl, C., 1995. 'Licht auf Abwegen', Spektrum der Wissenschaft, 5, 56-67 (Black hole animation at www.iwr.uni-heidelberg.de)
- de Vries, A., 2000. 'The apparent shape of a rotating charged black hole, closed photon orbits and the bifurcation set A4', Class. Quantum Grav., 17 (1), 123-144
- de Vries, A., and Schmidt-Kaler, T., 2002. 'Black hole tunnel phenomenon', Phys. Rev. D, 65, 104022
Weitere Links:
- Andrew Hamilton's Homepage mit einer Animation der Umkreisung eines Schwarzschildschen Schwarzen Lochs.
- Black Holes FAQ Liste von Ted Bunn.
| © de Vries 2003 |
|
|